What Is the Potential Difference Across Each Capacitor? How to Find the Difference?

Because the charge (Q) is equal and constant, the voltage drop or potential difference across the capacitor is dependent on the capacitor value, V = Q/C. A lower capacitance value results in a bigger voltage drop, whereas a large capacitance value results in a smaller voltage drop.

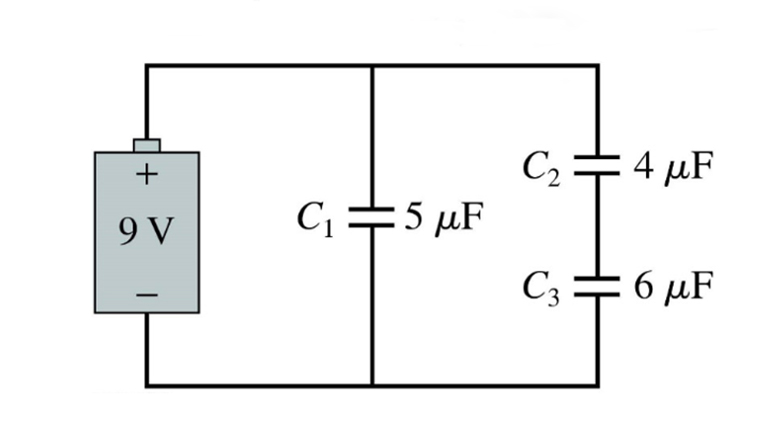
A capacitor is a critical component in an electrical circuit. Like other components (resistors, inductors), it provides resistance to current passage through it. The voltage drop across a capacitor is proportional to its charge and is uncharged at the start.

What Is the Potential Difference Across Each Capacitor?

In the absence of an external voltage source, a capacitor is simply a neutral conductor (before charging). When an external voltage is applied across a capacitor, however, it begins to store electric charges within it. The voltage across a capacitor is now proportional to its electric charge.

The voltage across a capacitor changes as the charge on it changes. As a result, when a capacitor is charged, the voltage across it rises. When a capacitor is fully charged, the voltage across it becomes constant. When we remove the external battery, the capacitor begins to discharge. 

What Is the Potential Difference in Capacitors?

When capacitors are connected in parallel, they have the same potential difference across each other, and the parallel technique adds the stored charges. Charge flows away from the e.m.f. and divides in proportion to capacitance.

When capacitors are connected in series, the overall capacitance is smaller than the sum of the individual capacitances of the series capacitors. When two or more capacitors are linked in series, the overall effect is that of a single (equivalent) capacitor with the sum total of the individual capacitors’ plate spacings.

How Do You Find the Potential Difference Across Each Capacitor?

The method for finding the potential difference across each capacitor is different for parallel and series connections. 

Capacitors in a Series Connection

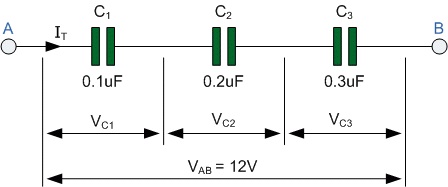
C₁ is linked to the left-hand plate of the second capacitor, C₂, whose right-hand plate is connected to the left-hand plate of the third capacitor, C₃, in the series circuit above the right-hand plate of the first capacitor, C₁. In a DC-connected circuit, this series connection means that capacitor C₂ is effectively separated from the circuit.

As a result, the effective plate area has shrunk to the smallest individual capacitance connected in the series chain. As a result, the voltage drop between each capacitor will differ based on the various capacitance values. Then, using Kirchhoff’s Voltage Law (KVL) to the preceding circuit, we obtain:

V_AB=V_c1+V_c2+V_c3

V_c1=Q_T/C₁, V_c2=Q_T/C₂, V_c3=Q_T/C₃ [Q_T=Total Charge]

Capacitors in a Parallel Connection

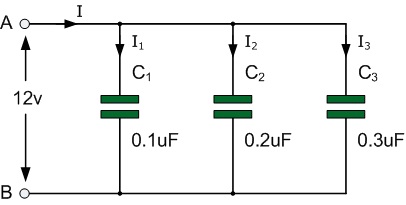
The voltage (Vc) applied across all capacitors linked in parallel is the same. Then, capacitors in parallel are connected with a common voltage supply, yielding:

V_AB = 12V = V_C1 = V_C2 = V_C3

The capacitors C₁, C₂, and C₃ are connected in a parallel branch between locations A and B in the following circuit.

The Formula for Voltage Drop Across Capacitor

Voltage Across an Uncharged Capacitor

A capacitor with no charge has no voltage drop. Because of Q=0 for an uncharged capacitor, and thus the voltage V=0.

Voltage Across a Capacitor During Charging

The equation for the voltage across a charging capacitor at any moment t during charging an AC capacitor of capacitance C with a series resistor R is,

V(t) = Vs (1 – e^-t/τ) ……. (1)

The time constant of the series RC circuit is, τ =RC, and the maximum voltage of the external battery is Vs.

Voltage Drop Across a Completely Charged Capacitor

After a long period of charging, the capacitor reaches saturation. The voltage drop across it reaches its highest at this point. Vs is the maximum voltage across a capacitor. However, in practice, the voltage across the capacitor cannot be greater than the maximum voltage of the battery.

It should be a voltage of V₀. If Q is the maximum charge on the capacitor, the formula for maximum voltage across the capacitor is V₀=Q/C. Then we have Q=CV₀. This is a common formula for calculating the voltage across a capacitor.

Voltage Across Capacitor During Discharging

If the external battery is now removed, the capacitor enters discharging mode and the voltage drop across the capacitor begins to diminish. The voltage across the discharging capacitor increases to,

V(t) = V₀ e^-t/τ……… (3)

τ =RC denotes the time constant.

Conclusion

When a capacitor is completely charged, a potential difference (p.d.) exists between its plates. The larger the area of the plates and/or the smaller the distance between them (known as separation), the greater the charge that the capacitor can carry and the greater its capacitance.