Why Base Current is Weak Then Collector Current? [Answered]

Transistors, the backbone of electronic circuits, operate on principles governed by intricate equations. If you’ve ever wondered why the base current is weaker than the collector current, you’re about to embark on a journey into the world of transistor equations and dynamics.

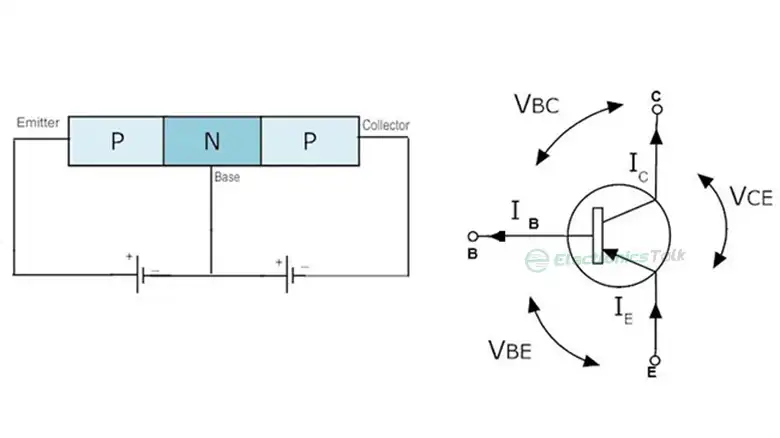
Concept of Base Current in Electronics

Base current (IB) is the current flowing into the base terminal of a transistor, initiating the flow of collector current (IC). Mathematically, this relationship is expressed by the equation:

I_c=β*I_B

where,

β represents the transistor’s current gain.

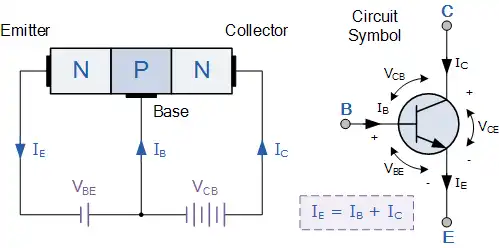
Figure: Base current in a transistor.

Relationship with Ic and IB

The equation I_E=I_C+I_B illustrates the interdependence of base, collector, and emitter currents. It emphasizes the weaker nature of I_B compared to the more substantial I_c.

Collector Current: The Powerhouse

Collector current (I_c) is the driving force behind the amplification capabilities of a transistor. Its influence on the output voltage is determined by the equation:

V_out=-β*V_in

This equation highlights the role of I_c in signal amplification.

Significance:

Expressed by the equation

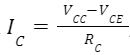
where V_CC is the collector supply voltage, V_CE is the collector-emitter voltage, and R_C is the collector resistor, I_c​ holds significant sway in transistor operation.

Weakness of Base Current

The equation I_c=β*I_B inherently signifies the limitations of I_B. Due to its dependence on β, the current gain of the transistor, I_B is weaker and imposes constraints on the overall efficiency of the transistor.

Impact on Efficiency:

The efficiency (η) of a transistor is defined by the equation:

This equation underscores the critical role of balancing I_B and I_C for optimal transistor efficiency.

Amplification Process of Base Current and Collector Current

Equations governing the amplification process shed light on the relationship between I_B and I_C. The gain (β) of a transistor, represented by the equation A_V=V_out/V_in​, is directly influenced by I_B.

Factors Influencing Current Strength

The equation I_B=I_CBO/β encapsulates the influence of semiconductor characteristics on I_B. I_CBO represents the reverse collector current, and β is the transistor gain.

Balance Between I_B and I_C:

Achieving balance is crucial, as highlighted by the equation I_C=β*I_B. Deviations from this balance can lead to inefficiencies and signal distortion.

Analogies and Metaphors

Analogies and metaphors enriched with equations provide a deeper understanding. Imagine I_B as the conductor orchestrating a symphony of electrons represented by I_C. This analogy aligns with the equation I_C=β*I_B, showcasing the conductor’s influence.

Comparing Base and Collector Currents

Quantitative analysis using equations reinforces the disparity between I_B and I_C. The graphical representation of I_B and I_C​ magnitudes visually demonstrates their relationship.

Conclusion

The intricate relationship between I_B and I_C in transistors unravels when viewed through equations. The mathematical underpinnings provide a nuanced understanding, emphasizing the importance of balancing these currents for efficient and reliable transistor operation.

Additional Questions May Ask

How is base current defined in a transistor?

Base current (I_B) is the current flowing into the base terminal of a transistor, initiating the flow of collector current (I_C). This relationship is expressed by the equation I_C=β*I_B.

What is the role of collector current in transistor amplification?

The collector current is the driving force behind the amplification capabilities of a transistor. Its influence on the output voltage is determined by the equation V_out=-β*V_in.​

How does the efficiency of a transistor relate to base and collector currents?

The efficiency of a transistor is defined by the equation η=P_out/P_in. This equation underscores the critical role of balancing I_B and I_C for optimal transistor efficiency.